U-критерий Манна-Уитни – непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно.
Метод был предложен в 1945 году американским химиком и статистиком Фрэнком Вилкоксоном. В 1947 году он был существенно переработан и расширен математиками Х.Б. Манном (H.B. Mann) и Д.Р. Уитни (D.R. Whitney), по именам которых сегодня обычно и называется.
Ограничения критерия Манна-Уитни
1. В каждой выборке должно быть не менее 3 наблюдений: n1,n2 ≥ З; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.
2. В каждой выборке должно быть не более 60 наблюдений; n1, n2 ≤ 60.
Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа – разные) или очень малое число таких совпадений.
Гипотезы U - критерия Манна-Уитни
H0: Уровень признака в группе 2 не ниже уровня признака в группе 1.
H1: Уровень признака в группе 2 ниже уровня признака в группе 1.
Помним. что 1-й выборкой (группой) называем тот ряд значений, в котором значения, по предварительной оценке выше, а 2-й выборкой (группой) соответственно предположительно ниже.
Алгоритм расчета критерия Манна-Уитни
1.Объединить все данные в единый ряд, пометив данные, принадлежащие разным выборкам.
2.Проранжировать значения, приписывая меньшему значению меньший ранг (значению 21 приписываем ранг 1). В случае равных значений признака у нескольких единиц каждой из них присваивается среднее арифметическое последовательных значений рангов. Например, три числа 31 занимают в едином ранжированном ряду 5. 6 и 7 место (ранг). Следовательно, каждой из них присваивается ранг равный (5+6+7) / 3= 6. Всего рангов получится (n1 + n2) = 15+15=30.
3. Подсчитать сумму рангов отдельно для каждой выборки.
4. Определить большую из двух ранговых сумм.
5. Определить эмперическое значение Uэмп по формуле:
Uэмп = n1·n2 + nx·(nx + 1)/2 – Tx,
где Uэмп – это численное значение критерия, n1 – объем выборки №1; n2 – объем выборки №2; Tx – большая из двух ранговых сумм; nx – объем максимальной выборки: nx= max(n1, n2).
Uэмп = 15·15 + 15·(15 + 1)/2 – 299 = 46
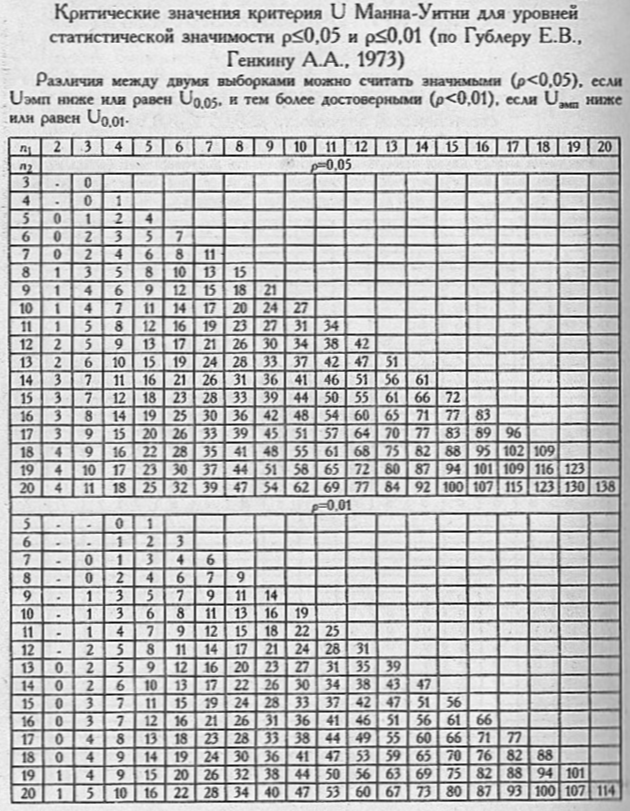
6. Определить критическое значение из специальной таблицы – Uкр. Для определения Uкр нужно учесть объемы выборок (n1, n2) и уровень статистической значимости (р), который отражает степень точности вывода о наличие различий.
В психолого-педагогических исследованиях приняты два уровня точности: р≤0,01 – вероятность ошибки 1%; р≤0,05 – вероятность ошибки 5%.
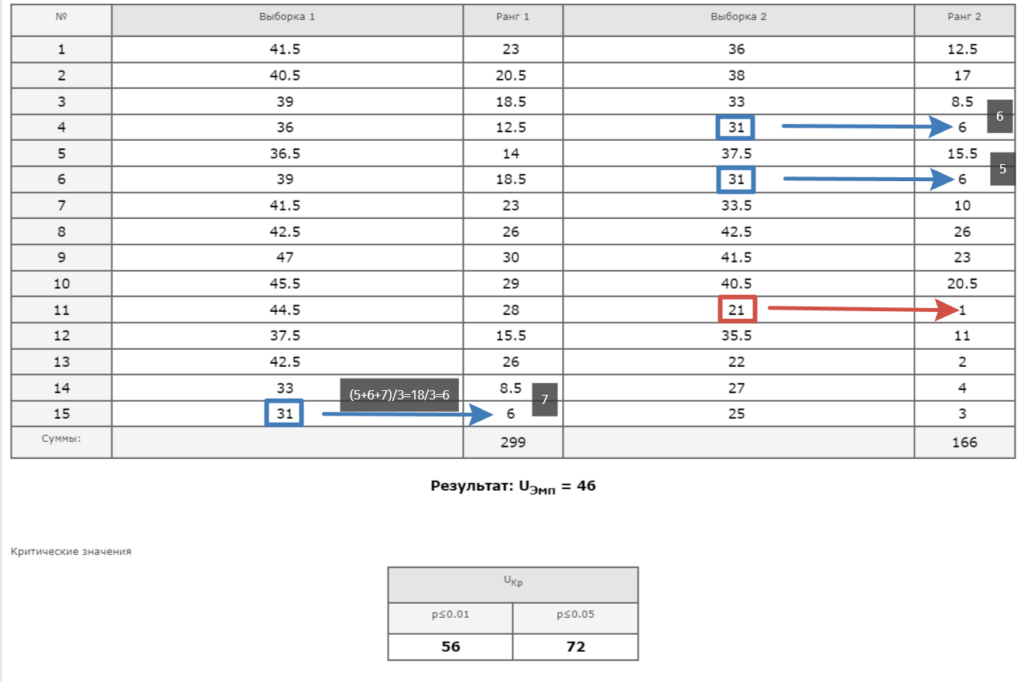
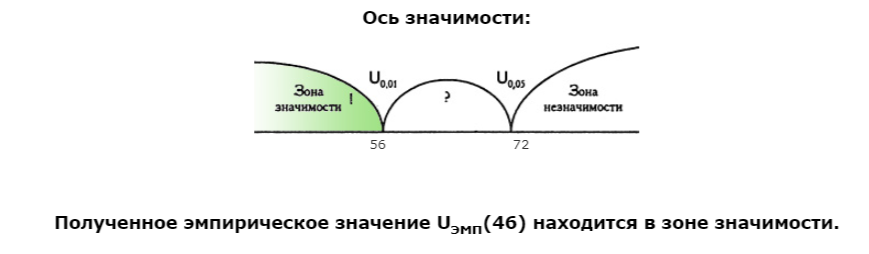
Сравнить полученное эмпирическое значение Uэмп с критическим значением Uкр. Если Uэмп > Uкр(0,05). H0 принимается. Если Uэмп ≤ Uкр(0,05) H0 отвергается. Чем меньше значения U, тем достоверность различий выше.
Автоматический расчет U-критерия Манна-Уитни
- https://www.psychol-ok.ru/statistics/mann-whitney/index.html
- https://medstatistic.ru/calculators/calcmann.html
- https://www.socscistatistics.com/tests/mannwhitney/default2.aspx
- https://www.statskingdom.com/170median_mann_whitney.html
- https://planetcalc.com/7858/
- https://statziki.com/Mannwhitneyu
- https://math.semestr.ru/corel/mann-whitney.php
- https://www.omnicalculator.com/statistics/u-test
Для анализа результатов тестирования в ходе эксперимента применяем критерий дважды:
- входное тестирование в контрольной (КГ) и экспериментальной (ЭГ) группах, где должны показать отсутствие различий в группах по изучаемому признаку;
- итоговое тестирование в этих группах должно продемонстрировать различие по изучаемому признаку.
Поскольку U-критерий Манна-Уитни является непараметрическим критерием, то в отличие от t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых выборок.
Аналогом U-критерия Манна-Уитни для сравнения трех и более групп является Критерий Краскела-Уоллиса.
Критерий Краскела-Уоллиса – непараметрический статистический критерий, используемый для сравнения 3-х и более независимых выборок по количественному или порядковому признаку.
Критерий был разработан американскими математиками. Уильям Краскел и Аллен Уоллис представили критерий в своей работе «Use of ranks in one-criterion variance analysis» в 1952 году. Отсюда и название критерия.
Критерий Краскела-Уоллиса подходит для сравнения небольших выборок. Желательно, чтобы в каждой выборке было не менее 5 наблюдений.
Допустим, вы измерили время реакции трех групп и хотите узнать, есть ли разница между ними. Чтобы выяснить это, теперь вы используете H-тест (тест Краскала-Уоллиса).
Гипотезы для теста Краскала-Уоллиса следующие:
- H0: Между выборками 1, 2, 3 и т. д. существуют лишь случайные различия по уровню исследуемого признака.
- Н1: Между выборками 1, 2, 3 и т. д. существуют неслучайные различия по уровню исследуемого признака.
Если тест Крускала-Уоллиса значим, это указывает на то, что по крайней мере одна из групп отличается от других. Однако сам тест не сообщает вам, какие группы отличаются друг от друга. Для этого необходимы последовательные попарные сравнения.
Тест Фридмана для повторных измерений
Критерий Фридмана является непараметрическим аналогом однофакторного дисперсионного анализа для повторных измерений. Данный критерий является распространением критерия Т Вилкоксона (Уилкоксона) на большее, чем 2, количество условий измерения. Разработан американским экономистом нобелевским лауреатом Милтоном Фридманом (Milton Friedman).
Он позволяет проверять гипотезы о различии более чем двух (т.е. от 3-х и до 100) повторных измерений по уровню выраженности изучаемой переменной.
Критерий более эффективен, чем дисперсионный анализ в случае малых выборок (до 30 объектов в выборке) и распределений, отличных от нормального. Он основан на ранжировании повторных измерений для каждого объекта выборки. При справедливости нулевой гипотезы значения статистики Фридмана (критерия Фридмана) малы, т.е. эмпирический критерий меньше, чем критический. И это означает, что различия случайны и недостоверны.
Критерий применяется для сопоставления показателей, измеренных в разных условиях (c>=3) на одной и той же выборке из n испытуемых. Критерий Фридмана позволяет установить, что величины показателей от условия к условию изменяются, но при этом не указывает на направление изменений и в этом смысле он похож на критерий знаков.
Например: Способность группы людей решать проблемы одинакова или различна утром, днем и вечером. Он используется для проверки различий между группами , когда зависимая переменная является порядковой. Этот тест особенно полезен, когда размер выборки очень мал.
- Нулевая гипотеза H0 = {между полученными в разных условиях показателями (т.е. между проверяемыми выборками) существуют лишь случайные различия}.
- Альтернативная гипотеза H1 = {между полученными в разных условиях показателями (т.е. между проверяемыми выборками) имеются существенные неслучайные различия}.
